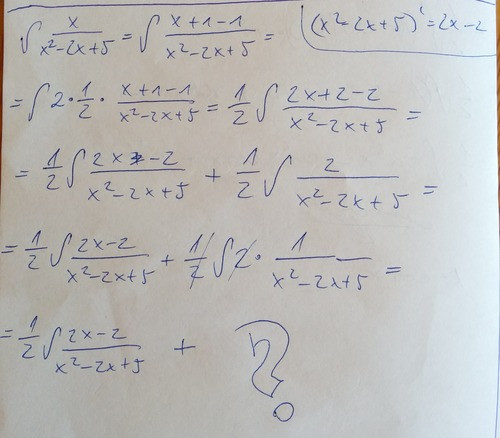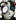Új hozzászólás Aktív témák
-

Gyb001
senior tag
Én sem tudtam hogy kell kiolvasni. Szóbelin leírtam papírra. Majd azt mondtam hogy ez a tranzitivitás, szimetria, antiszimetria...
-

pityaa23
senior tag
szerk: megoldódott a probléma.
-
Én nagyon sokat szívtam a linalg vizsgával
 Szóbeli, kapsz két tételt, kimondod, bebizonyítod mindkettőt az a kettes. 52db A4-es oldal a tananyag, de ömlesztett formában, kb. olvashatatlan, másból nem lehet tanulni, tragikus
Szóbeli, kapsz két tételt, kimondod, bebizonyítod mindkettőt az a kettes. 52db A4-es oldal a tananyag, de ömlesztett formában, kb. olvashatatlan, másból nem lehet tanulni, tragikus  Régebben 2 félévnyi anyag volt, de amikor bejött a Bsc-Msc rendszer akkor összepréselték egybe a tárgyat.
Régebben 2 félévnyi anyag volt, de amikor bejött a Bsc-Msc rendszer akkor összepréselték egybe a tárgyat. -

Gyb001
senior tag
Én is szeretném megköszönni mindenkinek a segítségét.


Hozzásegítettetek 30 Kredithez (Anal 1,2 Dimat 1,2 Valszám, Numerikus anal és egy ráadás négyes matek szigorlat)
Ugyan nem sok hsz-t írtam, de rengeteget olvastam ezt a fórumot. És így az utolsó matekos tárgyam vizsgája után egész megszerettem a matekot.Még egyszer köszönöm.
(Nem bme-s vagyok, de csak itt találtam jó képeket.)
-
válasz
 Cucuska2
#4785
üzenetére
Cucuska2
#4785
üzenetére
Anal3 elso resze integralas volt, masodik resze tobbvaltozos analizis.
Anal2 asszem derivalas def alapjan, derivalas minden mas modon stb. Anal1 meg hatarertek, konvergencia, ilyesmi. Elotte matalap, ott ilyen becslesekkel, polinomos dolgokkal, meg egyebekkel foglalkoztunk.
Szobeli vizsga hal istennek csak anal1-2-bol volt, az eleg fos volt. Bizonyitasokat magyarazgatni, baahh de utaltam

Anal4-ben fogalmam sincs mi lesz, de ezen a vonalon az az utso targy

-
Koszi meg egyszer az itteni segitseget, anal3 pipa, johet az anal4

-

TDX
tag
-
válasz
 Doky586
#4778
üzenetére
Doky586
#4778
üzenetére
A két egyenlet nálam: [a-egyenlet] [b-egyenlet] [alternatíva]
Win7 esetén: [a-egyenlet] [b-egyenlet] [alternatíva]
Helyes eredmények: [kép] [kép]

-
-
Tudom hogy jól csinálta, ezért mutattam hogy az androidos RealCalc ugyanerre hibásan számol (vagy legalábbis más logika szerint), akárcsak a Win7 és szinte mindegyik Android és PCs progi, pl excel)
De a másik egyenletet viszont valóban jól számolta a RealCalk.
Leírok két egyenletet amit átrendezés és kiegészítés nélkül egyetlen számológép sem képes mindkettőt helyesen megoldani(!):a.: (-32)^(2/5) = 4
b.: -32^(2/5) = -4Egyik esetben vagy error-al elszáll vagy át kell alakítani ezen formára az egyenletet.
Másik esetben muszáj elétenni egy 0 -t hogy helyesen oldja meg.
Ezen kétfajta számológép-típus létezik. -

nagybá
senior tag
válasz
 tomrRRR
#4773
üzenetére
tomrRRR
#4773
üzenetére
B-t úgy kellene, hogy a kérdéses tartományon integrálod a sűrűségfüggvényed ( ami jelen esetben két integrál összeadásából adódik), majd leosztod az egész tartományon vett integrállal. (végeredmény értéke 7/8-ad lesz)
Várható érték: Melyik az az érték amitől jobbra és balra 1/2-ed a függvény alatti terület értéke és ott milyen értéket vesz fel -> 1szerk.: De amúgy rajzold le ilyenkor a függvényed és sokkal átláthatóbb lesz a dolog.
-

tomrRRR
senior tag
Sziasztok!
Valaki megtudná oldani ezt a feladatot, fizetnék is érte ha úgy van, nagyon fontos lenne hétfőn vizsgázok. (Matek tanáromnak nem volt ideje megmutatni.)
-
Sajnos ez egy speciális eset hogy a (-32)^(3/5) = -(32^(3/5)) el, azaz nem tudni a végeredményből hogy a számolóprogram szoftvere valójában helyesen számolt-e. Egy jobb formulát kéne kitalálni és tesztelni azt a RealCalc programot. Nekem az a tippem hogy a zárójel bezárásakor kiszámolja az értéket, behelyettesíti és elfelejti hogy ott zárójel volt.
A kétség onnan ered hogy a -3^2 értékre 9 et ad hibásan, akkor is ha a 3 és ± gombot használom és akkor is ha úgy írom be hogy 5-8= majd négyzetre emelés. Mindkétszer hibásan pozitív 9 az eredmény. De a matematikusival ellentétben ez a informatikusi mentalitás szerint a helyes eredmény.
"hatvanharom osztva harom szor he't"
Nyilván a műveleti sorrend balról jobbra halad azonos preferenciájú műveletek közt. De a szorzás osztás megelőzi az összeadás kivonást stb.És itt a különbség hogy az informatikus a negatív jelet a szám részeként értelmezi nem mint műveleti jelet; a matematikus pedig műveleti jelnek tekinti amit csak a hatványozás szorzás osztás után kell elvégezni..
-

axioma
Topikgazda
válasz
 Doky586
#4769
üzenetére
Doky586
#4769
üzenetére
En amit leirtam az ahogy beirtam a szamologepbe... csak lusta voltam kepet csinalni, feltoltogetni. Azaz 32 [+- gomb] [x^y gomb] (3/5) [itt megjelenik, hogy 0.6] es = jel. Az -8.
Az informatikus nem tudom miert ne ugyanezt gondolna a -3^2-rol jo, csak magamrol nyilatkozok, de a precedenciat csak kene tudni es annak megfeleloen kodolni (=leirni).
Ha arrol van szo, hogy hatvanharom osztva harom szor he't, akkor is helyzetfuggoen irsz 63/3*7 vagy 63/(3*7)-t.
A zarojelekkel teljesen egyetertek (kulonos tekintettel azon kreten nyelvekre, ahol a << es >> shiftelo utasitasok a legalacsonyabb precedenciaval futnak, pedig valahol a szorzas es a hatvanyozas kozotti az "erzesre" besorolasuk - na ezzel spec. szivtam mar parszor...)
A legutolso linked eleg durva, de en ezt olyasmi hibanak erzem, mint amit te fentebb gondoltal rolam hogy elrontottam (a kepletleiras nem tukrozi, hogy milyen aktualis ertekre milyen muveleti gombot nyomtunk).
Ha azt irom, hogy 3 [+- gomb] [negyzetre emeles], akkor (-3) van a kijelzon amikor emelem negyzetre, es 9 lesz az eredmeny. Ha azt irom (a kitorolt tartalomra), hogy - 3 [negyzetre emeles] [egyenlo], akkor a kijelzon a - (pontosabban 0-) nem jelenik meg, csak az, hogy 3 es elvegzodik a negyzetre emeles (kiirva: 9), majd az =-re kiertekelodik az eleje, lesz -9. [Termeszetesen ha ugy allitjuk elo a -3-at, hogy - 3 [egyenlo], es utana jon a negyzetre emeles, akkor az megint rendesen 9 lesz. -
-
így ahogy most írtad le teljesen mást jelent!
ekkor a műveleti sorrend miatt a hatványozás megelőzi a kivonás műveletet.. ezért kellett a -32 t zárójelbe tenni. (ebben is nagy különbséget látok: a matematikusok teljesen másképp értelmezik ezt mint az informatikusok/számítástechnikusok: mennyi a -3^2 ? a matematikus szerint -9 az informatikus szerint 9 ... )
Ezért inkább használjunk több zárójelet, még ha felesleges is..
-

axioma
Topikgazda
-
Az előző képen mindkettő formulában negatív szám gyökvonása szerepel(?), mégis (vizsgán használható) zsebszámológépeken tesztelve az eredeti formában szinte kivétel nélkül megoldhatatlannak tartják és error-t adnak, amíg a másik formába átalakítva kivétel nélkül megadják a helyes választ... (a valós számok halmazán)
Gyökvonás: ahogy látszik ha van gyökvonás a formulában akkor helyesen számolnak, akkor van hiba amikor nincs gyökvonás jel, csak tört számmal való hatványozás (ami -elvileg- ugyanaz lenne..

-

axioma
Topikgazda
válasz
 Doky586
#4763
üzenetére
Doky586
#4763
üzenetére
1. nem ertem az elnezeskerest, nem tortent semmi
2. Sejtem, mi lehet a problemad: mivel negativ valos szamok eseten az altalanos gyokvonas kivezet a valos szamkorbol, ezert egyszerubb az egeszet komplex feladatnak kezelni, legalabbis ugy tunik, az altalad emlitett programok igy tesznek... De ez csak annak kerdese, hogy mit feltetelezunk egy negativ szam gyokvonasakor. Lehet, hogy bizonyos esetekben valos parameternel azt varnank, hogy van-e valos gyok, es abban az esetben azt megkapni, de ez nem a matematika oldalan kerdes (ott a gyokvonas vagy valos vagy komplex gyokvonas, es ez a feladatnal mindig egyertelmu), hanem tulajdonkeppen az adott programok probalnak intuitive segiteni a kezelonek, hogy ha mar nem adta meg hogy milyen eredmenyt var, akkor kitalaljak, hogy hogyan ertelmezzek.
Nyilvan ha azt irtad volna, hogy (-32+0*i)^(3/5), akkor nem lepodsz meg, hogy komplex eredmenyt kapsz, mert az egy jelzetten komplex szam. A negativ valos hatareset, hogy most valos akart direkte lenni. Egy szot a program iroinak vedelmeben: mivel a valos szamkoron beluli paratlan kitevos gyokvonasnal az elojel nem valtozik, szerintem nem nagy hiba feltetelezni, hogy aki a valos gyokot akarja az a minuszt kiemeli es a maradek gyoket keri el. Persze ha a -32 mar egy keplet eredmenye, akkor ezert a kiemelesert mar kuzdeni kell... de megoldhato.
A szamologep meg ugy muxik ahogy te varod, mert (a tobbseguk) nem szamol komplex szamokkal, csak a valos terben keres megoldast. Sztem a szamologep a (-32)^(1/4)-re nem fogja azt mondani, hogy -(32^(1/4)), hanem hibat (nullaval osztast). Bar szamologepnel ugye logaritmuson keresztul mukodik (nem vizsgalja, hogy racionalis-e a kitevo, nyilvan 2. es 5. gyokot se keplettel vagy kozelitessel von). -
válasz
 Cucuska2
#4764
üzenetére
Cucuska2
#4764
üzenetére
Elvi kérdés volt mint írtam...
De az XP, Google, WolframAlpha FŐ megoldása miért nem ez...:

Valami olyan szabály miatt van előrébb a komplex megoldás a valós számú (-8) előtt amit nem ismerek.Sőt bizonyos számológépek a (-32)^(3/5) beírásakor hibáznak a műveleti sorrendel és ennek az eredményét mutatják: -(32^(3/5)), ami hibás, de véletlenül ugyanazt az eredményt adja...
-
Akkor elnézést kérek..
Eszerint csak a WolframAlpha működik hibásan és kitünteti figyelmével az egyik komplex megoldást a sok közül..
és a Google is. -

axioma
Topikgazda
válasz
 Doky586
#4761
üzenetére
Doky586
#4761
üzenetére
Hol merul fel a "principal"-sag? Attol fugg.
Nyilvan arcsin eseten az elso periodusba [0,2*Pi) eso megoldasokat szoktak megjeleniteni, de pl. tangensnel a -Pi/2, Pi/2 koze eso ertek a logikusabbnak tuno (ert.tart. nem folytonos plusz itt kihasznalhato a monotonsag meg lehet me'g peldakat adni).
A konkret esetben ahol negativ valos szambol vonsz paratlan gyokot, es csak egy valos gyok van de a feladat definiative komplex, en ugyanugy a legkisebb nemnegativ szogelfordulasu gyokot adnam meg. De ez csak ugymond sajat szeperzek, sokkal fontosabb a dontesnel az, hogy mire hasznalod. -
Az világos hogy több megoldás van, de melyik a Fő (principal?) megoldás, vagy van a principal/fő szónak jelentése a matematikában?
Gondolom a 'principal' megoldás a következőnél az x=30, de ugyanúgy megoldás a x=2190 is..
(deg): sin(x)=1/2De az előző (-32)^(3/5) példánál mi/melyik a 'principal' ? (nem számszerűen)
Vagy a sin(x)=1/2 példánál:
Tanárnő: -Pistike, mennyi az x?
Pistike: - az kérem szépen 2190
Tanárnő: -Tökéletes! kiváló a válasz, zseni vagy Pistike!
-

axioma
Topikgazda
válasz
 Doky586
#4757
üzenetére
Doky586
#4757
üzenetére
Komplex szamok eseten gyokvonasnal a vegeredmeny a teljes halmaz, ami teljesiti: altalaban trigonometrikus alakban, azon belul is parameteresen irva a szoget: alfa+k*2*Pi/7 (k=0,1,..,6)
Gondolj arra, hogy hogyan adod meg egy sin alfa = 0.5 alaku egyenlet eredmenyet! Ott is lesz benne, csak ott tetszoleges k egeszre, egy k*2*Pi resz.
-
-
Sziasztok! Nekem is egy érdekes elvi kérdésem van.
Ha nincs kihangsúlyozva hogy egy képlet milyen eredményét keressük akkor a principal (=fő) megoldást keressük vagy a valós számok halmazán értelmezett megoldást..?Példa: (-32)^(3/5) képletnek a fő megoldása nem esik a valós számok halmazába, de van egy megoldása a valós számok halmazán is, de azt kis átrendezés után lehet csak kiszámolni zsebszámológéppel. (A fő megoldást offline csak XP-vel kaptam meg)
Ennél csak az 'jobb' ha olyan képletnek kell a végeredménye aminek nincs a valós számok körében megoldása, mint pl: (-6)^(0.7) [link]
-

tomrRRR
senior tag
Sziasztok!
Egy kis segítséget szeretnék kérni az alábbi feladatokban?
MATEK Valszegszám. eloszlásVárható értéke 1400, szórás 400.
P(ξ<900)=? Fi((900-1400/400)= Fi(-1.25)=FI(1.25)= 0.8944 ? (az a kérdés hogy ha negatív a Fi akkor nem kell kivonni 1et belőle ?
P(1000<ξ<1500)=? Fi(1500-1400/400) - Fi(1000-1400/400) = Fi(0.25) - Fi(-1) ???
P(ξ>800)=? Ezt nem tudom hogyan kell. -
Sziasztok! Ujra egy integralos pelda, nem tudom hol csusztam el, de a vegen a (-1)^(5/2) hulyesegnek tunik


-

artiny
őstag
Morfologiai szures, hogyan jott ki ez a lezaras?
Dilatáció erózió lezárás, hogyan jott ki.... -

peter9228
aktív tag
válasz
 #36268800
#4741
üzenetére
#36268800
#4741
üzenetére
Szia!
Megtett út = (v0+v1)*t/2, ebből kijön, hogy mennyi idő kellett hozzá, amiből ki tudod számolni a gyorsulást, ami alapján kijön a kérdésre a válasz. Nekem kb. 25 méter jött így ki.
-

#36268800
törölt tag
[Physics for dummies]
Sziasztok!Elnézést kérek először is, hogy a matek topicba (is) kiírom a kérdésemet, de a fizika topic nem tűnik ilyen aktívnak és gondoltam a matekosok is tudnak erre az egyszerű kérdésre válaszolni. (A feladat tuti egyszerű, csak nekem nincs nagyon hozzá agyam, meg már néhány oldalnyi feladatmegoldáson túl vagyok..)
Az alábbi feladatot hogyan kell megoldani? Valaki levezetné nekem szépen?
Egy egyenletesen gyorsuló autó 80m úton növelte a sebességét 10m/s-ról 20m/s-ra.
Mekkora úton érte el előzőleg a 10m/s sebességet, ha nyugalmi helyzetből indult, s gyorsulása végig állandó volt?Köszi előre is! Ebbe sajnos most beletört a bicskám, bár lehet, hogy csak fáradt vagyok.

-
-
Sziasztok! 3 feladatban kérném segítségeteket, újra

1. feladat
Megcsináltam, de nem tudom, hogy helyes-e a megoldásom.
2. feladat
A vége nem tiszta, nem tudom, hogy mi lesz az 1/(x^2 -2x +5)-el
3. feladat
Sin^4(x)-et kéne integrálni, már minden szarral próbálkoztam, de nem akar épkézláb eredmény kijönni
-

Cucuska2
addikt
Én még nem nagyon voltam olyan vizsgán, ahol szükségem lett volna számológépre. Ha pedig mégis rettentő olcsmány számok jöttek ki, elneveztem őket betűkkel, majd a végén hánytam vissza a papírra az eredményt, persze nem kiszámolva, hanem formulával. Ilyenért a 4 félévem alatt még sosem haraptak - bár a környezete mindig jó volt.
A számológép pedig numerikusan közelít, attól nem tudnál meg sokat.
-

cocka
veterán
még számológépet se vihetek
Akkor ez valami elte, bme vagy hasonló lesz, mert más helyeken azért engedni szokták. Na nem mintha akkora segítség lenne a számológép. Nyilván ésszerű határokon belül használható, de amúgy meg hiába viszel olyan számológépet, ami kiszámol neked pl. egy határozott integrált, ha egy határozatlant nem tudsz, akkor baszhatod. A számológép meg többnyire nem írja ki, hogy hogy jutott el az eredményig.
Ezért is tartom bődületes ökörségnek a számológép tiltását. A számológép tiltásával gyakorlatilag annyit lehet elérni, hogy a rutinszerű számolásokat is papíron vagy fejben kell elvégezned, ami jelentős időveszteség, főleg ha valakinek jól megy a matek és van hozzá affinitása (LOL, jó ezt egy matekos fórumba írni), de fejszámolásban nem annyira gyors.
A programozhatót és grafikust tényleg célszerű tiltani, de egy natúr tudományost felesleges.
-
Sziasztok! Hogy lesz az elso kifejezesbol a masodik?


(Elso kifejezes szamlaloja 4-es)
-

cocka
veterán
válasz
 ToMmY_hun
#4724
üzenetére
ToMmY_hun
#4724
üzenetére
Köszönöm. Mondjuk úgy, hogy kétszer kellett újraolvasnom, mire valamelyest felfogtam, de a normál eloszlással se mostanában foglalkoztam. LOL
de lesz különbség
Ja én is arra gondoltam, hogy le kéne programozni, aztán kiderülne, csak kérdés, hogy hány kísérlet kéne ahhoz, hogy objektíven meghatározható legyen, hogy melyik variáció a hatékonyabb. Avagy mekkora ez a különbség.
-

ToMmY_hun
senior tag
Központi határeloszlás tétel szerint önmagában egyenletes eloszlást mutató, egymástól független folyamatok kimenetét aggregálva az eredő egyre inkább a normális eloszlást közelíti. Ez alapján ha hat kockával egyszerre dobsz, akkor már nem tekinthető egyenletesnek az eloszlás. Ha normális eloszlás generálása a cél, akkor dobj hat kockával, majd normalizáld az eredményt a kívánt tartományra. A hatból kettőt kiválasztva nem fog jelentős mértékben eltérni az egyenletes eloszláshoz képest, de lesz különbség. Kísérletezéshez javaslok valamilyen matematikai programot, én Matlabot szoktam használni. Mondjuk ennek a bizonyítására még az Excel is jó.

-

cocka
veterán
Hi!
Lehet hogy ez ilyen gagyinak tűnő kérdés, de kombinatorikában vagy valószínűségszámításban sose voltam jó. Szóval kvázi dobókockajáték, de nem is feltétlen nevezném játéknak.
Tegyük fel, hogy vmilyen szempontból kedvező eset, ha 7-nél többet dobunk két kockával. De a kérdés lényegét tekintve lehetne akár úgy is fogalmazni, hogy 8-nál vagy 9-nél dobunk többet két kockával, akkor oké.
A kérdés:
Melyik esetben nagyobb a valószínűsége annak, hogy kedvező értéket kapunk?
1. Dobunk két kockával.
2. Dobunk 6 kockával és ezekből vakon választunk ki kettőt.
3. Dobunk 6 kockával, majd megismételjük a 2. folyamatot, hogy növeljük az esélyeinket. Azaz kétszer ismételjük meg a 6 kockával dobást, de végül ugyanúgy random választunk ki kettőt a második 6-os szériából.
Szóval a kérdés az, hogy mely esetben nagyobb a valószínűsége annak, hogy a kedvező értéket dobjuk (ami mondjuk 7-től 12-ig bármi lehet) vagy netán egyik esetben sem nagyobb, hanem egyforma?
-

skoda12
aktív tag
Gyökvonás nem jelenhet meg csak úgy, szóval vagy lemaradt valami vagy véletlen került fel a táblára.
Viszont nincs is rá szükség mivel az 1 / (1 - u^2) már alapintegrál. Artanh vagy arcoth lesz a primitív függvény értelmezési tartománytól függően. Tehát második lépésként u = gyök(2)*x helyettesítéssel alapintegrálra lehet hozni a kifejezést és bekerül egy 1 / gyök(2) szorzó.
Másik megoldás a nevezőt két tényező szorzataként felírni, utána parciális törtekre bontás és két alapintegrált fogsz kapni, mindkettő ln(valami) primitív függvénnyel. -
Sziasztok! Gyakon az elso es az utolso kifejezest irtuk le, probalok rajonni, hogyan kovetkezik egymasbol. Tudja esetleg valaki?
(Utsonal is van integral jel, azt lehagytam)

Azt is ertem hogy mire megy ki a jatek, 1/gyök(1-x^2) elerese a cél, de hogy mikent jutok el odaig...
-
Basszus, koszi!
 tanultam regebben, de agyam mint a szita
tanultam regebben, de agyam mint a szita 
-
Sziasztok! Ez itt a modulo 5 maradek osztaly, maradek oszt. szorzassal. Kerdesem hogy hogyan jonnek ki a tablazat elemei?


-

skoda12
aktív tag
válasz
 peter9228
#4710
üzenetére
peter9228
#4710
üzenetére
A paraméteres alakból érdemes kiindulni. Itt csak azt kell meghatároznod, hogy időegység alatt az omega és fí szögek mennyit változzanak. Az omega szögnek gyorsabban kell változnia, mint a fínek, ha azt szeretnéd, hogy a kis kör mentén többször körbefusson a görbe, amíg a nagy kör mentén csak egyszer fut végig.
Az hogy lesz-e benne látható szakadás attól függ, milyen egységben változik az idő (és a tőle pl lineárisan függő szögek). Minél kisebb az időegység változás, annál folytonosabbnak fog tűnni a görbe. -

peter9228
aktív tag
Sziasztok!
Van egy tóruszom, és annak az oldalán szeretnék végighúzni egy görbét, ami önmagában záródik. Valami ilyesmire gondoltam: [link] Adottak a tórusz adatai (középpont, és a két sugár) Bemenet egy időpillanat, amire vissza kéne adni a görbe egy pontját. Szerintetek hogyan kéne kiindulni? Én arra gondoltam hogy egy vektort eltolok a nagyobb körvonalra, elforgatom a kör érintőegyenese mentén, és megnézem hol metszi a tóruszt. Az eltolás helye és a forgatás nagysága függne a kapott bemenettől. Ez így működőképes lehet, vagy nagyon nehéz lenne azt megoldani, hogy ne legyen benne szakadás?
-

Jester01
veterán
De van és ezt az idézett leírás is alátámasztja. Az, hogy te nem hallottál még róla az egy dolog

Lásd még: "The general consensus among math people is that "multiplication by juxtaposition" (that is, multiplying by just putting things next to each other, rather than using the "×" sign) indicates that the juxtaposed values must be multiplied together before processing other operations. But not all software is programmed this way, and sometimes teachers view things differently."
Vagy:
"multiplications expressed implicitly by juxtaposition will be taken to bind more strongly than the divisions or explicitly expressed multiplications."
Vagy:
American Mathematical Society make a difference and in their order of operations we have
1. Parentheses
2. Exponents
3. Multiplication by juxtaposition
4. Multiplication and division from left to right
5. Addition and subtraction -

Apollo17hu
őstag
válasz
 AeSDé Team
#4703
üzenetére
AeSDé Team
#4703
üzenetére
Szorzás és osztás nem asszociatív, tehát jobb.
-

emiki6
veterán
válasz
 AeSDé Team
#4703
üzenetére
AeSDé Team
#4703
üzenetére
Ismereteim alapján inkább a bal.
-

Jester01
veterán
válasz
 AeSDé Team
#4703
üzenetére
AeSDé Team
#4703
üzenetére
Mi még úgy tanultuk, hogy ha nem írod ki a szorzásjelet akkor azt kell előbb elvégezni. Tehát a bal

Az egyik kommentben idézték is a számológép leírását, ami ugyanezt mondja.
-

AeSDé Team
őstag
Vélemény?

(Szerintem a jobb a helyes) -

Jester01
veterán
válasz
 ricinus13
#4700
üzenetére
ricinus13
#4700
üzenetére
Ez inkább fizika kérdés mert tudni kellene hozzá az egyenletet

Valami exponenciális csökkenés rémlik nekem, nézzük gugli mit mesél róla:
T(t) = Tenv + (T0 - Tenv) * e^-rtAhol r valami állandó. Ennek az értékét kell kiszámolni, hogy aztán vissza tudjuk helyettesíteni.
T(30) = 20 + (240 - 20) * e^-30r = 130
110/220 = e^-30r
ln(0.5) = -30r
r = -ln(0.5)/30Mennyi idő múlva lesz 30 fok:
20 + (240 - 20) * e^-rt = 30
220 * e^(ln(0.5) * t / 30) = 10
e^(ln(0.5) * t / 30) = 10 / 220
ln(0.5) * t / 30 = ln(10 / 220)
t = 30 * ln(10 / 220) / ln(0.5) ~ 134 perc -

ricinus13
senior tag
válasz
 ricinus13
#4700
üzenetére
ricinus13
#4700
üzenetére
Kifogytam a szerk. időből, még egy van amiben kéne segítség. Ugye az megvan ha egy lineáris diff egyenlet valami ilyen alakú: y''+y'+y=0 akkor annak van egy szép általános megoldó képlete, ám nekem egy olyanom van ami nem 0-val egyenlő hanem 10e^x, ennek hogy van a megoldása?
Új hozzászólás Aktív témák
- AMD vs. INTEL vs. NVIDIA
- HiFi műszaki szemmel - sztereó hangrendszerek
- GoodSpeed: Te hány éves vagy?
- Xbox Series X|S
- Gitáros topic
- Projektor topic
- CES 2026: olcsó, kompakt, többportos GaN töltőt kínál a Lenovo
- Kodi és kiegészítői magyar nyelvű online tartalmakhoz (Linux, Windows)
- Telekom otthoni szolgáltatások (TV, internet, telefon)
- Torrent meghívó kunyeráló
- További aktív témák...
- ASUS X455L LAPTOP i3-5100U 12GB!! DDR3 GeForce 820M 2GB 128GB SSD
- ASUS X541U LAPTOP i3-7100U 4GB DDR4 GeForce 920M 2GB 256GB SSD ÚJ AKSIVAL!
- ASUS F751L LAPTOP i5-5200U 8GB DDR3 GeForce 940M 2 GB 256GB SSD ÚJ AKSIVAL!
- Bontatlan Asus ExpertBook B5602CVN i5 13 gen/8GB/512GB, bontatlan gyári dokkolóval eladó!
- Tarr Béla A Curson Collection Blu-ray díszdoboz eladó! Új
- Apple iPhone 16 Plus 128GB, Kártyafüggetlen, 1 Év Garanciával
- Új és régi konzolok Okosítása és Szoftveres szintű javítása - Már 12.52 FW-s PS4-ek is!
- Lenovo P500 - 1650-2690 v3 akár 12 mag/24 szál, 16-32GB DDR4 RAM, 490W 80+gold táp, számla, 6 hó gar
- ÁRGARANCIA!Épített KomPhone Ryzen 7 5700X 32/64GB RAM RX 7800 XT 16GB GAMER PC termékbeszámítással
- Akciós kisWorkstation! Dell Precision 3560 i7-1165G7 4.7GHz / 16GB / 512GB / Quadro T500 2GB FHD 15"
Állásajánlatok
Cég: PCMENTOR SZERVIZ KFT.
Város: Budapest
Cég: Laptopszaki Kft.
Város: Budapest








 )
)

 Szóbeli, kapsz két tételt, kimondod, bebizonyítod mindkettőt az a kettes. 52db A4-es oldal a tananyag, de ömlesztett formában, kb. olvashatatlan, másból nem lehet tanulni, tragikus
Szóbeli, kapsz két tételt, kimondod, bebizonyítod mindkettőt az a kettes. 52db A4-es oldal a tananyag, de ömlesztett formában, kb. olvashatatlan, másból nem lehet tanulni, tragikus  Régebben 2 félévnyi anyag volt, de amikor bejött a Bsc-Msc rendszer akkor összepréselték egybe a tárgyat.
Régebben 2 félévnyi anyag volt, de amikor bejött a Bsc-Msc rendszer akkor összepréselték egybe a tárgyat.


![;]](http://cdn.rios.hu/dl/s/v1.gif)























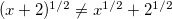 egyenlőség nem jó.
egyenlőség nem jó.