Új hozzászólás Aktív témák
-
-
kovisoft
őstag
-
kovisoft
őstag
válasz
Bozso68
#6285
üzenetére
Nekem a szögfüggvényes rész nem világos. Ha jól értem, egységnyi sugarú gömbnek tekintjük a Földet. De akkor a sin(radián(KH)) és cos(radián(KH))-ból kapott Px és Py koordináták az egyenlítő mentén érvényesek. Ha ezekhez még hozzávesszük a sin(radián(ÉSZ))-ből számított Pz-t, akkor már nem a gömb felszínén lévő (Px, Py, Pz) pontot kapunk, hanem az egyenlítőtől érintő (azaz a Föld forgástengelyével párhuzamos egyenes) mentén mérjük fel a Pz-t, tehát egy jócskán űrbéli pontot kapunk. Valahol a Px, Py-nál hiányolok egy cos(radián(ÉSZ))-gel való osztást, hogy visszakerüljünk a gömbfelszínre. Vagy rosszul látok valamit?
-
axioma
Topikgazda
válasz
Bozso68
#6289
üzenetére
Betoltam excelbe a 3 radianos koordinatat, de elegge korlatos a pontossaga ugye, a solver ennel nem tudott jobbat:
0,951501866 0,307906023 0,726566977
ahol a tavolsagok
0,004499634
0,004499642
0,004499633
ez sztem neked mar pont tul nagy pontatlansag. Azert 64 biten valoszinuleg lehet jobbat...szerk. Python pl. [link] (nem hasznaltam de a scipy -t be lehetett volna elore is tippelni hogy tud ilyet).
-
Bozso68
őstag
Köszi, átnézem a linket.
Sajnos országosan több, mint száz pont van, az elég nagy távolság és elég pontosan kell számolnom közöttük (már amennyire gömb a Földünk). Első gondolatom volt normál koordinátákként kezelni a GPS koordinátákat de x-y irányban más a lépték, ezután hagytam is a gondolatot. -
axioma
Topikgazda
válasz
Bozso68
#6287
üzenetére
Ezt talaltam, van megoldas (sugar hasonlit a heron-keplethez, kozeppont szamitasara is irtak vmit), de nekem eleve gyanus volt hogy ez azert nem feltetlen jon ki egyszeruen)
[link]
Amugy nem lehet hogy ezeket eleg lenne siknak tekinteni, olyan kicsi me'g ekkora tavolsagnal a gorbulet?Szerk. Ah, megtalaltam a szorzatot! De ahhoz elobb kell a 3 pont sikjanak normalisa. De ez is ott van a linken.
En - ha ez nem hazi feladat amihez levezetes kell - siman megprobalnam hogy a wolframalpha-nak be tudom-e adni, talan szelsoertek-keresest lehet csinalni azon hogy R sugaru gombok kozul amik atmennek a 3 ponton melyik minimalis sugaru (4 ismeretlen 3 egyenlet, negyzetes tagok kiesnek, hat nem tudom ki lehet-e hozni hogy az R az egyik fuggvenye...)
A programozo enem meg irna egy egyre finomodo keresest a kulonbseget valami nagy szorzoval sulyozva, a sugarat meg siman, hm, lehet hogy az excel celertek-keresese is tudhatja... -
Bozso68
őstag
Köszi!
Igen, eredetileg helyesen vontam ki, utána kínomban fordítottam előjelet a kivonásokban (ez maradt a leírásomban véletlenül). Mivel minden negatív előjelet kapott a végeredmény változatlan maradt.Szerk:
HA jól értelmezem a mostanában megismerteket? A szögfüggvénnyel kapott három pont (A, B, C) -ból kapott két különbségvektor (B-A, és C-A) szorzata adja meg az általuk meghatározott sík normálvektorát, ami jelen esetben áthalad az origón, egyben a három pont köré írható kör sugarán. Ez nem akar kijönni sehogy. -
axioma
Topikgazda
válasz
Bozso68
#6285
üzenetére
A kivonasnal a vegpontbol vonjuk ki a kezdopontot, az biztos forditva van felirva, de most ennyibol meg nem mondom hogy csak ez-e a hiba. Nem ertem hogyan jon ide a vektorszorzas, de 3D miatt inkabb nem mondok semmit, nagyon reg volt.
(Bocs, kozben szerkesztgettem, inkabb nem hagyok itt hulyeseget...) -
Bozso68
őstag
Sziasztok!
3 GPS koordináta köré írható kör középpontját keresem.
Excelben vezettem végig a számításokat, de valahol nagyon nem stimmel valami, és ebben kérem a segítségeteket, hol hibáztam.
Az eljárás, matematikai fogalmak nélkülözésével:
Az adott 3 koordináta:
A ÉSZ 46,79058, KH 17,70968
B ÉSZ 46,91098, KH 18,07602
C ÉSZ 46,39225, KH 18,14634
Koordinátákká alakítás: Px=sin(radián(KH)), Py=cos(radián(KH)), Pz=sin(radián(ÉSZ)) P (A, B, C)
Ax=0,95261, Ay=0,304194, Az=0,728856
Bx=0,950646, By=0,310279, Bz=0,730293
Cx=0,950264, Cy=0,311445, Cz=0,724079
B-A vektor:
Bx-Ax=0,001964, By-Ay=-0,00608, Bz-Az=-0,00144
C-A vektor:
Cx-Ax=0,00235, Cy-Ay=-0,007251, Cz-Az=0,004777A két vektor szorzataként
Kx=-3,9489E-05, Ky=-1,27563E-05, Kz=2,99025E-08 jött ki.
Ez sehogy se mutat az eredeti 3 pont közepébe.Hálásan köszönöm, ha valaki végig tudná értelmezni, és a hibá(k)ra rávilágítani.
-
axioma
Topikgazda
Varj, en nem sugarat mondtam. Metszd el az egeszet, es szamold meg, hany metszespont van azok kozul a pont felett. Ehhez kell:
0. elek tarolasa ugy, hogy (x1,y1,x2,y2) alakban x1<=x2
1. e'l ellenorzese hogy az x=P[0] metszi-e (x1<P[0]<x2, egyenloseg ugyis kulon kezelendo)
2. a skalarszorzatos modszerrel megallapitod, hogy P jobbra van-e az igy allo szakasztol (ha igen, az e'l felette metszi)
3. hany felette metszo van
Az xy teglalap nem teljesen vilagos, de ugy ertettem, hogy a P benne van az el altal meghatarozott teglalapban, az biztosan nem elegendo vizsgalatra (pl. egyszeru stopp-tabla es a kozepso pont, egy ilyen elet se fogsz talalni). -
coco2
őstag
válasz
g.peter23
#6280
üzenetére
Az a felezési idő 5 év azt jelenti, hogy az Y tengelyed 2-es logaritmus szerint van. 1,2,3,4 helyett 2,4,8,16 és úgy tovább. Az X tengelyed lineáris. A csökkenési egyenest egyenesen húzhatod abban a koordináta rendszerben (meredekség 5 év egység jobbra, 1 egység le). Ha interpolálnod kell, 2-es logaritmus szerint számolhatod. A logaritmus számolásnak utána kell majd kotorni
-
coco2
őstag
Igen, határérték vizsgálattal valamennyi poligon él eleve kizárható. Még azt tudom megtenni, hogy külön ránézek vízszintesen, aztán külön függőlegesen, hogy a vizsgált vonal mentén hány éllel kell elboldogulnom. Néhánynál tudok gyorsított vizsgálattal átlépni, mert csak a darabszámuk számít azt eldönteni, hogy a végén a vizsgáló sugár bent vagy kint marad-e a poligonon. Azokat az éleket tudom átlépni, amiknél a végpontok alapján az x-y téglalap a vizsgálandó vonalat elmetszi, de a pont még nincsen abban a tartományban. Aztán amiknek a végpontjai alapján az él már abban az x-y tépglalapban van, ahol a pont, ott részleteket számolok. Azt még részletek számolása nélkül tudom eldönteni, hogy vízszintes vagy függőleges vizsgálattal kell-e kevesebbet számolnom. És kb ennyit sikerült találnom gyorsításként. Szerintem ez már elég alapos lesz, ezt fogom leprogramozni. A segítséget köszönöm, az eredeti problémám megnyugtatóan megoldódott.
-
axioma
Topikgazda
Azt konnyu megallapitani, h melyik elet metszed [ha az e'let nemcsokkeno x szerint ta'rolod, koztuk legyen a P-e']. Ezutan mar csak az a kerdes, 'alatta' van-e a P pont az egyenese'nek, arra meg akkor bevetheted @kovisoft modszeret. Ezeket nekem konnyunek tunik osszeszamolni.
Nyilvan a fuggoleges e'lek igenyelnek egy kis plusz if-elgetes.
Ha programot irsz mert sokszor kell ugyanarra a poligonra mas-mas P-kre valaszolni, es nem eri el a sokezres nagysagrendet a poligon csucsainak szama, akkor az erintett csucsok kivalasztasahoz csinalhatsz elofeldolgozast: adott x letezo erteknel mely indexuek kisebb bal vegpontuak, illetve masik tombben x-nel mely indexuek nagyobbak, akkor egy halmazmetszet a vizsgalando indexek listaja. -
coco2
őstag
Hmm, pechemre a körüljárás mégsem működik mindenféle poligonra. Ha van mondjuk egy téglalapom, és abban egy konkáv beszögellés az egyik sarkánál, közel az egyik oldalhoz, a pont pedig a másik oldalon van, akkor a beszögellő élnél a pont külsőnek látszik
Úgy tűnik, tényleg vizsgálósugarat kell küldenem a poligonra, az lesz a leggyorsabb kód. -
coco2
őstag
Köszönöm a tippeket mindenkinek.
@axioma: Természetesen olyasmire gondoltam
Ami a poligon metszését illeti egyenesekkel, az vizuálisan egyszerűnek tűnik, de a számolása meglehet nagyon sok. Kotorászni kell az éleket adó x-y pontok és arányaik között azt megállapítani, hogy egy adott y=konstant esetén X-eken végig haladva hol metszem a poligont, ha a pont esetleg nagyon közel van (ha bőségesen benne van a poligonban, akkor mezei határérték ellenőrzéssel gyorsítani tudok, de nincs mindig olyan luxusom). Lehet konkáv is az a poligon temérdek sok beszögelléssel, ergo minden alkalommal minden egyenest számításba kell vennem. Persze egy poligont 3szögekre bontani sem kevés művelet, szóval még filozom rajta, hogy na most aztán mitévő legyek @kovisoft: Ez a körüljárási irány szerint mindig befelé van a pont vektora egész ügyes meglátás, tetszik
Még az is lehet, hogy a poligont egyenesekkel vagdosás helyett inkább ezt használom. Működik ez poligonra is, mindenfélére, és egyszerűnek tűnik.@TDX: Az a sanda gyanúm, nem sikerült megértenem
Még gondolkodom rajta. -
TDX
tag
A fentebb írt válaszok mellett könnyű kihozni egy megoldást baricentrikus koordinátákkal. A baricentrikus koordinátázás annyi dióhéjban, hogy ha veszel egy X pontot a síkon kívül, és van ABC három nem egy egyenesre eső pontod a síkon, a vektor az X-ből A-ba mutató vektor és hasonlóan b, c, akkor a sík azon pontok halmaza, amikhez αa+βb+γc vektor mutat X-ből, ahol α+β+γ=1.
Ez komplikáltnak tűnhet, de ebben a rendszerben az ABC háromszög pontjai pontosan azok lesznek, amikre α, β és γ is nemnegatív. Belső pontok pedig azok, melyekre mindhárom szigorúan pozitív.
Ezt pedig a következőképp lehet alkalmazni annak a kiszámolására, hogy belső pontról van-e szó. Az X-szel nem törődünk itt, hanem csak a síkban dolgozunk, legyenek a három csúcs koordinátái (x1,y1), (x2,y2), (x3,y3), és legyen P-é (x,y). Ekkor keressük a fentebbi α,β,γ-t.
Behelyettesítve gammára, és keveset számolva kijön a következő egyenlet (sajnos nem tudom, hogy hogy lehet könnyen mátrixokat leírni itt):
(x1-x3 x2-x3) (α) (x-x3)
(y1-y3 y2-y3) (β) = (y-y3)Ezt alfa és bétára megoldva ha olyan értékek jönnek ki, hogy mind alfa, mind béta és mind (1-α-β) nemnegatív, akkor P pont rajta van a háromszögön, és ha mindhárom érték pozitív, a belsejében van.
-
kovisoft
őstag
így van, nem csak háromszögre, hanem más konvex poligonokra is igaz, mert ekkor a poligon előáll az oldalegyenesei által meghatározott félsíkok metszeteként. Egy konkáv polinomnak viszont van olyan oldalegyenese, amelyik "kettévágja" a poligont, azaz az általa meghatározott mindkét félsíkba esnek belső pontok.
-
axioma
Topikgazda
válasz
kovisoft
#6271
üzenetére
Koszi, en voltam bena h minek az elojele a skalar szorzat elojele. De legalabb most mar nem keresni fogom hanem remelhetoleg emlekezni ra [mintha olyan sokszor jonne ilyen feladat szembe... amugy vszinu azzal kevertem h konvex poligonra is me'g igaz, de konkavra ertelemszeruen [geom szemlelet iranyzekkal] nem feltetlen...
-
kovisoft
őstag
Oldalvektorokkal való skaláris szorzat pont nem jó ilyesmire, az kb. csak annyi árul el, hogy az adott pontnak az oldalvektorral alkotott háromszöge hegyes vagy tompaszögű lenne-e (azaz a pont az oldalvektor kezdőpontjához képest "előre", az oldalvektor végpontja felé, vagy "hátra" helyezkedik-e el).
A normálvektorral való skaláris szorzat előjele mondja meg, hogy az adott pont az oldalvektor egyenese által definiált két félsík közül melyik oldaliba esik.
Ha körbejárva a háromszög oldalait, mindig ugyanarra az oldalamra esik a pont, akkor be tudtam zárni a körbejárással.
Szerk: Ja, bocs, elküldtem frissítés előtt. Látom, hogy közben szerkesztetted.
-
kovisoft
őstag
Azt kell megnézni, hogy a háromszög oldalait körbejárva a p1 pont mindig ugyanúgy balkéz vagy mindig ugyanúgy jobbkéz felé esik-e. Ha igen, akkor a pont a háromszög belsejében van.
Ehhez venni kell sorban a háromszög oldalvektorainak (A->B, B->C és C->A) a normálvektorát, amit mindhárom esetben ugyanúgy kell meghatározni (pl. mindig balra 90 fokot forgatva, azaz felcseréljük a koordinátáit és mondjuk mindig az x-nek az előjelét változtatjuk meg). Meg kell nézni az oldalszakasz kezdőpontjából a p1 pontba mutató vektor és a normálvektor skaláris szorzatának az előjelét. Ha az mindhárom esetben ugyanolyan előjelű, akkor a pont a háromszög belsejében van.
-
kovisoft
őstag
Legyen a két folyadék keverési aránya t és 1-t, azaz 1 ml keverékhez t ml-t veszek az A és (1-t) ml-t veszek a B folyadékból. Ekkor X*t + Y*(1-t) lesz 1ml keverék tömege, azaz az X*t + Y*(1-t) = Z egyenletet kell megoldani t-re, ahol nyilván csak a 0<=t<=1 esetet fogadjuk el megoldásnak:
(X-Y)*t + Y = Z
azaz:
t = (Z-Y)/(X-Y)A konkrét példádban: t = (18-20)/(6-20) = 2/14 = 1/7, azaz 1/7 mennyiséget kell venni a 6 mg/ml-es és 6/7 mennyiséget a 20 mg/ml-es folyadékból.
Ha fix mennyiséged van az A folyadékból, akkor ezt elosztod t-vel és megszorzod (1-t)-vel, így megkapod, hogy mennyi B folyadékot kell hozzákeverni a kívánt sűrűséghez.
Ismét a konkrét példádban a 100 ml A-hoz 100*(6/7)/(1/7) = 100*6 = 600 ml kellene B-ből, de annyi nincs, tehát úgy nem tudod előállítani a kívánt keveréket, hogy a teljes 100 ml A-hoz öntesz hozzá a szintén 100 ml B-ből. Fordítva megy a dolog, vagy akkor is, ha A-ból nem használod fel a teljes mennyiséget, csak legfeljebb az 1/6-át, vagy esetleg ha B-ből van még utánpótlásod.
-
Sziasztok!
Remélem jó helyen járok, egy képletet keresek és ehhez segítséget.
Egy célorientált számológép leprogramozásával vagyok most elfoglalva és ehhez kéne egy képlet.
Hogy könnyebb legyen a dolog, egy-egyben leírom, miről van szó.Adott egy folyadék (A), melyben X mg/ml eltérő anyag található. Továbbá van egy Y mg/ml eltérő anyagot tartalmazó folyadékom (B) is. A kérdés az, hogy hogyan lehet kiszámolni, hogy mennyit kell B folyadékból A folyadékba tölteni, hogy a kívánt Z mg/ml arányt megkapjam?
Egyszerű példa:
(A) folyadék = 100 ml, tartalmaz 6 mg/ml S anyagot.
(B) folyadék = 100 ml, tartalmaz 20 mg/ml S anyagot.
Mennyit kell B-ből beletennem A-ba, hogy S egyenlő legyen 18 mg/ml-el?Előre is köszönöm a segítséget!
-
axioma
Topikgazda
Pont ez. Barmelyikbe is kerul a legolcsobb, az lesz abbol a csomagbol ingyen. Tehat a cel a masik ingyenes maximalizalasa, amit ugy ersz el ha a 4. legdragabbat sikerul ingyenesse tenned, a dragak egybecsomagolasaval. Ertelemszeruen a 4. legdragabbnal dragabb konyvet semmilyen modon nem tudsz a 4-es csomag legolcsobbjava tenni.
-
looser
addikt
Sziasztok!
Felmerült bennem egy matematikai kérdés, mivel nem vagyok szakértője a területnek (ennek sem) így a próbálgatós módszerrel vettem végig a lehetőségeket. Ha erre esetleg van egyszerűbb recept, örömmel venném :-)
A helyzet a következő: a HVG online könyvesboltja 3+1 akciót hirdetett. Négy megvásárolt könyvből a legolcsóbbat ingyen kapod. Kinéztem nyolc könyvet, ilyenkor (ne számítsuk a posta vagy egyéb költségeket) a haszonmaximalizásálás elve miatt érdemes 4+4 -re különbontani a rendelést. A könyvek árai a következők: 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000 Ft. Azt gondolom, ha a négy legdrágább és négy legolcsóbb van egy pakkban, akkor lesz a legmagasabb a nyereség, vagyis az ingyen kapott könyvek értéke (5000+1000). Mi lenne a matematika módszere erre a problémára?
Üdv
-
#6260
axioma
Topikgazda
racskobalazs
#6259
axioma
Topikgazda
válasz
racskobalazs
#6259
üzenetére
Igen, valami ilyesmi, de persze egy csomo mindentol fugg, mi a jo strategia. Peldaul mennyire nagy a suly/sugar ertekekben a szoras [a szakaszhossz fedesenek kb. ez az a'ra, jo per 2]. Ha sok, akkor mohoval allitanek fel minimumot, es onnan elagazas-korlatozas. Ha a pontok vannak kevesen, velhetoen keves megoldas van eleve is, akkor teljes kereses backtrack. Es me'g mindig ott a felezessel dp is aka'r, bar ott ugyesen kell osztani [a ket pont kozott se mind1 hogy hol, hogy meglegyen az optimum].
-
#6259
racskobalazs
senior tag
racskobalazs
senior tag
Köszi szépen!
Igen, túllóghat ha úgy értetted, hogy a szakaszon kívül eshet-e még az adott lámpa sugarából, a lényeg csak az, hogy a szakasz belsejében legyen mindenhol "fedett". Az, hogy a végein kilóg az nem gond.
Hogy érted a lámpák sorrendjét? Kijelölök egy pontot, oda lerakok 1-et, és ahhoz választom a következőt, hogy jó legyen? -
#6258
axioma
Topikgazda
racskobalazs
#6257
axioma
Topikgazda
válasz
racskobalazs
#6257
üzenetére
OK, a napokig futas csak egy extremitas volt [plane ha a megiras/adatelokeszites ennel is hosszabb].
A tizes nagysagrendu valasztek az annyi+1 [uresen marad] valasztas per pont. Raadasul eros elagazas-korlatozassal. Bar en lehet h lampak sorrendjet generalnam, es keresnek hozza kov pontot. Mar ha a kezdes kitalalhato -> meddig kell fedni [szakasz, nem egyenes], ott tulloghat-e.
A grafalgo nekem ehhez nem jon ossze, valami dynamic programming megoldas johetne erre, jo allapot-tarolast kell kitalalni hozza. -
#6257
racskobalazs
senior tag
axioma
#6256
racskobalazs
senior tag
Szia, köszönöm a gyors választ!
Sorban válaszolok:
1. Lámpa típusokból valóban kb 10-es nagyságrendű féle van, viszont azokból korlátlan mennyiség állhat rendelkezésre. Minden lámpafajtának különböző lehet a sugara, de annak a fajtának akkor csak és kizárólag az. Nem kell minden pontot felhasználni ha épp úgy jön ki, és lámpából sem kell minden félét lerakni kötelezően. Egy ponton csak 1 lámpa lehet.
2. Egy térképrészletre (egyenesek) elég 1x megcsinálni, és viszonylag kis területen, csak "demonstrációs" jelleggel kell futnia. (Kis terület: <1000 (nagyon max <10.000) pont, az első tesztterületem 184 pontnyi méretű, ha a pontokat 10 méterenként rakom le az egyenesekre), viszont nem biztos, hogy örülnének ha napokat futna
3. Igen, valószínűleg bőven belefér, én azt mondanám, hogy akár 5-10% is, de ez nincs meghatározva (még).
Mennyiségek, kb lámpadarabszám<100, pontdarabszám<1000 (<10000) és amennyiben az inputot átalakítom úgy, hogy egyenesenként tárolja a pontokat, akkor szerintem mehet párhuzamosan is.Remélem ez segít, és nagyon köszönöm mégegyszer a választ!
-
#6256
axioma
Topikgazda
racskobalazs
#6255
axioma
Topikgazda
válasz
racskobalazs
#6255
üzenetére
Ha a pontok is meg a sugarak is fixek, es 'keves' lehetseges pont van a varhato lampaszamhoz kepest, akkor jo esellyel nincs megoldas.
Azt gyanitom, hogy ha ez a valo eletben van, akkor ennel jobban lehet a felteteleket korlatozni: 1. viszonylag keves tipusu lampa csak valamelyikbol/mindbol tobb 2. csak 1x kell megcsinalni, futhat 2 napot 3. nem kell pontosnak lenni pl 2% hiany/atfedes me'g elfogadhato
Mik a mennyisegek, es van-e jelentosege, hogy egyben fusson az osszes egyenes [lampa darabszamok] vagy lehet kulon-kulon optimalizalni? -
#6255
racskobalazs
senior tag
racskobalazs
senior tag
Sziasztok!
Gráfelméletes kérdésem / feladatom lenne, gondoltam kiírom ide hátha valaki foglalkozott már hasonlóval
Vannak pontjaim (X,Y) párként, valódi geokoordináták. Vannak "lámpáim" melyeknek vannak különböző adataik, amiből 2 fontos: világítási sugár, és "súly" (súly= valamilyen kalkulált súly, az ár, fogyasztás ilyesmik alapján, még nem találtam ki ).
A feladat az lenne, hogy ezekre a pontokra lámpákat rakva legjobban lefedjünk egy területet, úgy, hogy "az egy vonalon lévő" lámpák fényköre összeérjen és a legkisebb összsúly legyen a vége. (Egy vonalon lévő: nem messzebb egymástól, mint a fix ponttávolság ami szabadon választott viszont nem nagyobb mint a lámpák közül a legnagyobb fénysugár kétszerese (mert két lámpányi esélyem van a köztes távolságot lefedni)).
GeoGebra gyorsvázlat (nem precíz, de kb ilyesmire gondolok):
Látható, hogy lényegében csak az egy vonalon lévő lámpákra kell "figyelni", hogy ne lógjon bele a másikba és le is fedje a köztes távot. Valamint nem kell az összes pontot felhasználni, ha úgy jön ki, hogy jobb súlya van egy nagyobb lámpának, akkor köztes pontokra nem kötelező rakni.
Inputon is lehet variálni, ha az segíthet akkor talán a pontok mellé egy vonal ID-t is tudok szerezni, hogy melyik pont melyik "számú" vonalon fekszik.Van bárkinek ötlete, hogy lehetne nekiállni? Nekem az első két ötletem valami féle minimális feszítőfa, vagy valamilyen útkereső lenne, de egyiknek se tudom mit hogy kéne beadni.
Bárkinek van bármilyen ötlete hogyan lehetne ennek nekiállni?
Előre is köszönöm!
-
-
axioma
Topikgazda
Szerintem excelben menni fog a Solver-rel simplex beallitassal, csinalsz egy oszlopot a darabszamokra es megadod feltetelnek hogy binaris, csinalsz egy oszlopot arra, hogy mi lesz a darabszam amit kivalasztasz (szorzat a binarissal), csinalsz egy oszlopot arra hogy mi lesz az a'r (szorzat a binarissal), utobbi kettot az aljan szummazod, es a darabszamra megadod feltetelnek hogy >=5, mig a celertek meg a masik szumman minimum.
Amugy nekem a szinten 4.1 koltsegu 2,4,6 kombinaciot hozta ki. Azt nem tudom (nem latom jelentoseget azon kivul, hogy van-e megoldas vagy azt mondjuk hogy nincs), hogy az a'r maximumot hozza kell-e tenni, hiszen a minimalis arat keresed ha jol ertem, az most vagy 5 alatt van, vagy nem.szerk most latom sql-t irtal... akkor viszont igy elsore passz, gozom sincs letezik-e binaris szimplex beepitve barhol is
-
kovisoft
őstag
Ez eléggé úgy tűnik, mint a hátizsák probléma egyik speciális esete: a 0-1 hátizsák probláma, amikor is egy árus összes áruját vagy beletesszük a hátizsákba vagy nem. A hátizsák probléma NP-teljes, úgyhogy nem fogsz rá igazán gyors algoritmust találni. Konkrét algoritmusokért a neten keress rá a "hátizsák probléma" vagy "knapsack problem" vagy "0-1 knapsack problem" kifejezésekre.
-
crocy
tag
Hi,
lehet csak en bonyolitom tul ezt a dolgot(es/vagy hülye vagyok), egy sql tabla bejarasban kene kis segitseg(vagy vmi algo).
Szoval tegyük fel egy tabla rekordjaiban azt taroljuk, hogy egyes arusok mennyiert(összar), mennyi krumplit arulnak es egy arustol összes mennyiseget fel kell vasarolni.
Ekkor jön egy vasarlo, hogy ker egy listat, hogy kiktöl kell vasarolni, ha egy bizonyos megadott max összeg, min mennyiseg eseten a legjobban jarjon.Pl a lenti tablabol, max 5ft-ert min 5 kg arunal az optimalis, az 1 es a 4 rekord:
4.1ert (2.6+1.5) kap 5 kg krumplit.
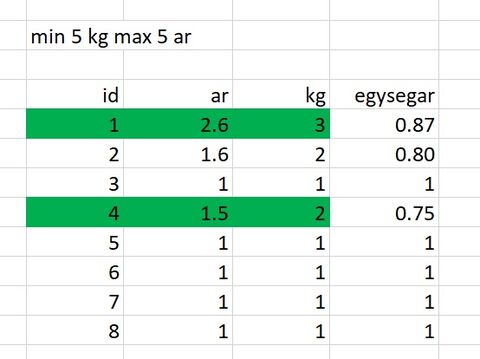
De ezt vmi tablabejaras alapjan, hogyan kapom meg? Elöször megprobaltam egysegar alapjan növekö sorrendben rendezni, majd kummulalni a sorokat. De mint a fenti pelda is mutatja nem feltetlenül a legolcsobb egysegaru rekordokbol jön ki az optimalis megoldas.
-
kovisoft
őstag
Azt nem mondanám, hogy egyszerűbb a módszer, mert én két skaláris szorzást javasoltam. Mindezt azért, mert nem csak az az eset állhat fenn, hogy mindkét sík egymás felé vagy egymástól kifelé néz. Az is lehet, hogy az egyik normálvektor a másik háromszögre néz, de amannak a normálvektora meg épp ellenkező irányba néz.
Pl. lehet, hogy a két háromszög síkja merőleges egymásra, az elsőnek a normálvektora befelé mutat, a másodiké kifelé, a két normálvektor pont merőleges egymásra, pusztán a két normálvektorból nem tudjuk eldönteni, hogy mi a szituáció.
-
-
kovisoft
őstag
Mindkét normálvektorról külön-külön el tudod dönteni, hogy a másik háromszög felé mutat-e vagy ellenkező irányba. Mégpedig úgy, hogy kiszámolod az adott háromszög normálvektorának és egy ebből a háromszögből a másik háromszögbe mutató vektornak (pl. a másik háromszög 3. csúcsába mutató vektornak) a skaláris szorzatát. Ha ez a szorzat pozitív, akkor a normálvektor a másik háromszög felé mutat.
-
coco2
őstag
Sziasztok!
Egy térgeometriai problémán gondolkodom. Az eljárás a kérdéses, hogyan tudom eldönteni, hogy két sík egymás felé néz-e, vagy sem?
Van két térbeli háromszögem. A pontjaikat és a "külső" felületüket ismerem, a normálvektoraikat ki tudom számolni. A két háromszögről tudom, hogy nem egy síkban vannak, és hogy van egy közös élük (1-1 pontjuk azonos).
Azt szeretném tudni róluk, hogy a normálvektoraik összetartóak, vagy széttartóak-e?
Amerre gondolkodom, az a háromszögek 3. pontjának összekötése +2 háromszöggel egy gúlát építeni. Az eredeti háromszögek normálvektorai abban a gúlába vagy befele mutatnak, vagy abból kifele. Azt megállapítanom meg is válaszolná a kérdést. De még nem jöttem rá, azt hogyan tudom eldönteni?
Gondolkodom síkgeometriai módszeren, de még nem sikerült rájönnöm, hogyan tudom a kérdést síkgeometriára lefordítani.
Kotorászom a netet, és felírtam ezt a topikot. Bármilyen segítő tanácsnak örülni fogok.
Előre is köszönöm.
-
-
skoda12
aktív tag
válasz
Attix82
#6238
üzenetére
Ezt az összeget felírod az első n elemre, kiemeled belőle a 0,0001-et. Ami zárójelen belül marad arra felírod a mértani sor összegképletét és ez az egész <= 100. Ezt az egyenlőtlenséget átrendezéssel és logaritmussal megoldod n-re. A következő n-nél nagyobb egész lesz a megoldás az eredeti kérdésre.
-
#6237
föccer
nagyúr
Apollo17hu
#6236
föccer
nagyúr
válasz
Apollo17hu
#6236
üzenetére
A képlet ugyan az csak az előjelekre kell figyelni.
Nekem +50%-os változásnak tűnik így ránézésre.
üdv, föccer
-
#6236
Apollo17hu
őstag
Apollo17hu
őstag
Sziasztok!
Fura mód eddig még nem futottam bele ebbe a talán egyszerűnek tűnő problémába, és hirtelen nem is tudom hogy guglizzak rá, ezért fordulok hozzátok.
Excel-kimutatást készítek, ahol a trendeket is mutatni szeretném:
a tárgy időszaki érték bázis időszaki értékéhez képest történő elmozdulást határoznám meg százalékosan.A problémám az, hogyha mondjuk tárgy = -50 és bázis = -100, akkor milyen értéke lesz a növekménynek? A -100 -ról -50 -re történő emelkedés 50%-os növekmény lenne? És mi a helyzet akkor, ha -100 -ről +50 -re történik a növekedés?
Van erre vmi univerzális képlet?
-
kovisoft
őstag
válasz
HellGreg
#6233
üzenetére
"pl. 354-nél a 3 alaki értéke 3x100, valódi értéke 300. De ugye ez a két érték mindig ugyanaz?"
Nem, 354-nél a 3 helyi értéke 100, alaki értéke 3, a valódi értéke 300. Az alaki érték az maga a számjegy, azaz hogy mennyit kell venni az adott helyi értékből, hogy megkapjuk a valódi értékét.
-
-
HellGreg
őstag
Sziasztok. A fiam általános 3.-os, éppen beteg, és persze most tanulják a számok helyi, alaki és valódi értékét. Rákerestem a neten, hogy lehetne elmagyarázni neki. A helyi érték az nem gond (1, 10, 100...) de az alaki érték és a valódi érték között nem igazán értem a különbséget, pl. 354-nél a 3 alaki értéke 3x100, valódi értéke 300. De ugye ez a két érték mindig ugyanaz?
A feladat a könyvben meg ez volt: írj olyan 3-jegyű számokat, ahol a legkisebb helyi érték a legnagyobb alaki érték. Én úgy értem, hogy akkor 9-esre végződő háromjegyű számokat kell írni. Nem vagyok matekos beállítottságú, így lehet hogy hülyeségeket írok -
kovisoft
őstag
Elnézést, ha esetleg félreértem a problémát, de ha van két 3D forgatásunk, akkor ezek eredője is egy 3D forgatás lesz. Ha az x és y tengely körüli forgatást mátrix alakban felírjuk, akkor az eredőjük a két mátrix szorzata lesz (nyilván számít a forgatások sorrendje). Ennek a szorzatmátrixnak a sajátvektora lesz az eredő forgástengely, de ez most neked nem lényeges. A forgásszöget pedig megkapjuk a szorzatmátrix nyomából: (tr = trace, a főátlóban lévő elemek összege). Ha R a szorzatmátrix és theta a forgásszög, akkor:
tr(R) = 1+2cos(theta)
A szorzatmátrixot nyomához nincs szükség a komplett mátrix előállítására, csupán a 3 db főátló menti értéket kell hozzá meghatározni.
-
VoidXs
nagyúr
Sziasztok, hogyan lehetne optimálisan megtalálni a szöget két 3D elforgatás közt? Jelenleg azt csinálom, hogy az egységgömbön felveszem a nekik megfelelő pontot, és skalárszorzatból visszaszámolható a szög, ez viszont sok művelet. Lehetne gyorsabban? Az egy könnyítő tényező, hogy az egyik forgatás csak az x, a másik pedig csak az y tengely körül történik, de ezzel is csak a gömbre helyezésből csípek le 1-1 műveletet.
-
kovisoft
őstag
3+3 pont esetén az előző hozzászólásom alapján rögzített 2 ponttal összesen 8 ismeretlen koordinátánk van, erre van 8 másodfokú egyenletünk. Ennek az egyenletrendszernek a megoldását érdemes a rögzített pontoktól való távolságokkal kezdeni. Így minden ismeretlen pont y koordinátáját ki tudjuk fejezni az x koordinátából. Így marad 4 ismeretlenünk. Na innentől kezd igazán csúf lenni a dolog, de talán nem reménytelen.
A megoldhatóságnak elégséges feltétele lehet az, ha semelyik 3 pont nem esik egy egyenesre.
-
VoidXs
nagyúr
válasz
kovisoft
#6220
üzenetére
Köszönöm szépen a választ, ez már sokat segít. Az "összes pont relatív helye" alatt pontosan azt értettem, amit te is. A megoldások közül viszont bármelyik megfelelő, csak algoritmikusan elő lehessen állítani, így a megoldhatóság alatt azt szerettem volna kérdezni, hogy létezik-e olyan módszer, ami garantál bármilyen, a távolsági kritériumoknak megfelelő eredményt. Ha már csak az előállna, hogy 3 pontot tudunk rögzíteni, onnantól körök egyenletével a lehetséges helyeket végig lehet próbálni, és kellően kicsi számoknál (a gyakorlatban 2 <= N <= 8 és 3 <= M <= 21) ezeket még egy egyáltalán nem hatékony algoritmus is gyorsan megtalálja.
-
kovisoft
őstag
Először is tisztázzuk, hogy mit értünk az alatt, hogy "összes pont relatív helye". Gondolom, úgy kell érteni, hogy két rendszert egyformának tekintek, ha eltolással és forgatással egymásba átvihetők. Ez tulajdonképpen azt jelenti, hogy mindkét ponthalmazból kiválaszthatunk egy-egy pontot, amelyeknek a helyzetét rögzítettnek tekinthetjük. Legyen mondjuk az első halmazból kiválasztott pont a P(0,0), a másik ponthalmazból kiválasztott és tőle x távolságra lévő pont pedig a Q(x,0).
Ez tehát azt jelenti, hogy ha a két ponthalmazban lévő pontok száma N és M (N,M>1), akkor ezeknek a síkban 2N+2M koordinátája van, ezekből 4-et ismerünk (P-ét és Q-ét), tehát marad 2N+2M-4 ismeretlenünk.
A kölcsönös távolságokból pedig van N*M másodfokú egyenletünk, de mivel a P és Q pontok már rögzítettek, ezért ezek távolságát kihagyva marad N*M-1 egyenlet.
Biztosan nem lehet egyértelműen megoldani a feladatot, ha több ismeretlen van, mint ahány egyenlet, azaz ha 2N+2M-4>N*M-1. Ez pl. M=N esetén 4N-4>N^2-1, átalakítva N^2-4N+3<0, azaz ha N=2.
Ez nem jelenti azt, hogy ha legalább annyi egyenlet van, mint ismeretlen, akkor meg lehetne oldani, hiszen lehetnek összefüggő egyenletek, amikor az egyik egyenletet elő lehet állítani néhány másik lineáris kombinációjával.
-
VoidXs
nagyúr
Sziasztok, egy számomra nehéz feladattal akadtam el, amiről azt se tudom eldönteni, hogy egyáltalán lehetséges-e olyan módon, ami nem brute force. Van két ponthalmazom, és mindkét halmaz pontjairól ismert, hogy a másik halmaz bármely pontjától milyen távol van, de kizárólag ennyi információm van. Meghatározható-e ebből az összes pont relatív helye, és ha igen, hogyan?
-
axioma
Topikgazda
válasz
Fecogame
#6216
üzenetére
Tudomanyos alak vagy hasonlo ne'ven szokta'k emlegetni. Celja: latni a nagysagrendet. A bal oldalon mindig egy 1 es 10 kozti szam all, az E utan meg hogy 10 a hanyadikon (plusz/minusz is). Sokkal kezelhetobb mintha azt irom hogy 238842000. Ez most latod egybol hogy hany millio? Bezzeg ha igy irom hogy 2.38842E08 akkor latod hogy a 10^6-hoz kepest me'g ket nagysagrend, tehat majdnem 239millio. (Valamint a szamitogepes abrazolas - hasonlot csinal csak kettes szamrendszerben - praktikus okokbol csak az elso valahany, jellemzoen tizenpar tizedesjegyet orzi, a tobbi mar nem tud a szam pontossagahoz hozzatenni, mint fent is a vegere irtam harom 0-t, de ha ott 298 lenne az se valtoztatna erezheto mertekben azon az erteken, amit leir.)
-
Áfogat
csendes tag
Sziasztok!
Adott lenne egy, az általánosból kimaradt, gimibe tartó fiatal. Milyen könyvből lenne érdemes gyakorolnia a nyáron? Elsősorban nem az elmélet a lényeg, hanem példák kellenének, ezekből is a valóságból merített, realisztikus példákat részesíteném előnyben.
Ismertek olyan könyvet ahol főként a gyakorlás a cél (elsősorban könyv kellene, online csak akkor, ha nincs értelmes könyv)?
-
kovisoft
őstag
válasz
kovisoft
#6210
üzenetére
Közben rájöttem, hogy az F(7)=0-t is kérdezted:
Modulo p=7 a szóba jöhető a,b,c-k az 1,2,3,4,5,6. Ezek harmadik hatványai (modulo 7): 1^3=1, 2^3=1, 3^3=6, 4^3=1, 5^3=6, 6^3=6. Ezekből sehogyan sem tudsz venni kettőt, hogy azok összege a harmadik legyen (modulo 7), hiszen 1+1=2, 1+6=0, 6+6=5. -
kovisoft
őstag
Nézzük meg, mit is jelent az F(5)=12:
Modulo p=5 a szóba jöhető 1<=a, b, c<p értékek az 1, 2, 3, 4 lehetnek. Ezek harmadik hatványai (szintén modulo 5): 1^3=1, 2^3=3, 3^3=2, 4^3=4. Ezekből 12-féleképpen lehet előállítani az a^3+b^3=c^3 (mod 5)-öt: 1+1=2, 1+2=2+1=3, 1+3=3+1=4, 2+2=4, 2+4=4+2=1, 3+3=1, 3+4=4+3=2, 4+4=3. -
coco2
őstag
Sziasztok!
Ezen az oldalon valaki el tudná nekem magyarázni az F(5)=12 és F(7)=0 definíciós részt?
Amennyire megérteni tudtam az ott írtakat, az 5-nél kisebb prímekre (2 és 3) összesen 6 egyenletet lehet felírni, amik egyike sem egybevágó, nem hogy 12 egyenlet létezhetne, amiknek az eredménye egybevágó.
Mit néztem el?
-
axioma
Topikgazda
válasz
Csikter
#6207
üzenetére
Nem matematikai a kerdes, a teszt lehet szarul osszeallitva, de attol me'g ha egyszer definialtak hogy a tesztkerdes vagy 0 vagy 1 pont, es 50% azaz 10-bol 5 pont kell, akkor mind1 hogy mind a 10-ben csak 1-et ikszeltel felre, az akkor is jogosan 0 pont.
Normalis esetben ilyenkor az igen-nem kerdesek pont jol lefedik hogy mennyire ertette meg a jelolt a dolgot. Nem lehet oket szetvalasztani, mert akkor teljesen mast mernenek. Pl. mashogy megfogalmazott de egymasnak ellentetes allitasokat ha egyforman jelolsz, a tobbitol tok fuggetlenul azt bizony me'g nem erted megfelelo mertekben, jogos a 0 pont. -
Csikter
csendes tag
Sziasztok!
Lehet, hogy ez egy kicsit off topic.
Lenne egy problémám, amit saját kútfőből nem tudok megoldani. Ha tudnátok segíteni, nagyon hálás lennék.
A helyzet a következő:
Épp egy OKJ képzésen veszek részt, ahol belefutottam az első "ZH-ba".
Teszt, 10 kérdés, 50%-tól van meg, tehát 5 kérdésre kell jól válaszolni. Eddig ez viszonylag standard.
De mi van akkor, ha a kérdések úgy szólnak, hogy "jelölje meg az igaz, (vagy éppen hamis) állításokat", és egy kérdés alatt van nagyjából 8-10 állítás.
Ha egyet hibázol, az egész "kérdést" buktad. Mennyire etikus erre azt mondani, hogy 50%-tól? Mert amennyire az én limitált képességeimből kitelik, ha az összesen 70-80 állításból elhibázol mondjuk 6-ot rossz kombinációban, akkor buktad a teszted, pedig 92.5%-ra írtad. Szerintetek számokban kifejezve mi itt a valós minimum?
Köszi a segítséget! -
#6206
f(x)=exp(x)
őstag
f(x)=exp(x)
őstag
Hali!
Jó gráfelméletes könyvet vagy bármilyen anyagot tudtok ajánlani? -
kovisoft
őstag
Eleve abból indult ki a feladat, hogy a két egyenes egy síkban van. Egy egyenes a síkot két félsíkra osztja. Mivel nyílt félsíkokról van szó, ezek nem tartalmazzák magának az egyenesnek a pontjait. Úgy is mondhatjuk, hogy a síkot egy benne lévő egyenes erre a három diszjunkt részre osztja: két nyílt félsík és maga az egyenes. Ha tehát bármilyen ponthalmaz teljes mértékben az egyik ilyen nyílt félsíkban van, akkor annak nincs közös pontja a síkot felosztó egyenessel. Ha ez a ponthalmaz egy másik egyenes, akkor van ugye két egyenesünk ugyanabban a síkban, és ezeknek nincs metszéspontjuk, azaz párhuzamosak.
-
Zizus
friss újonc
Köszönöm a válaszokat, tisztul a kép.
Euklideszi geometria axiómarendszerét kell(ene) felhasználni. Az tiszta, hogy egy egyenes két félsíkra osztja a síkot. Az is megvan, hogy ahhoz, hogy párhuzamosak legyenek, egy síkban kell lenniük. Engem ez a nyílt félsíkos dolog zavar meg.
Tehát akkor, ha mindegyik a másik által meghatározott nyílt félsíkban van, akkor tulajdonképpen egy síkban vannak? -
kovisoft
őstag
Nem tudom, pontosan milyen axiómákat kellene használnod, de ha egy egyenes egy másik által meghatározott egyik nyílt félsîkban van, akkor nincs közös pontja a másik egyenessel. Két egyenes pedig akkor párhuzamos, ha egy síkban vannak és nem metszik egymást, azaz nincs közös pontjuk.
Úgy tűnik, tényleg vizsgálósugarat kell küldenem a poligonra, az lesz a leggyorsabb kód.
Ami a poligon metszését illeti egyenesekkel, az vizuálisan egyszerűnek tűnik, de a számolása meglehet nagyon sok. Kotorászni kell az éleket adó x-y pontok és arányaik között azt megállapítani, hogy egy adott y=konstant esetén X-eken végig haladva hol metszem a poligont, ha a pont esetleg nagyon közel van (ha bőségesen benne van a poligonban, akkor mezei határérték ellenőrzéssel gyorsítani tudok, de nincs mindig olyan luxusom). Lehet konkáv is az a poligon temérdek sok beszögelléssel, ergo minden alkalommal minden egyenest számításba kell vennem. Persze egy poligont 3szögekre bontani sem kevés művelet, szóval még filozom rajta, hogy na most aztán mitévő legyek 
Még az is lehet, hogy a poligont egyenesekkel vagdosás helyett inkább ezt használom. Működik ez poligonra is, mindenfélére, és egyszerűnek tűnik.
Új hozzászólás Aktív témák
- Dell Latitude E6410 i5 M560, Nvidia NVS 3100M 512MB GDDR3, 4Gb RAM, 250GB HDD, jó akku, számla gar
- ÁRGARANCIA!Épített KomPhone i5 12400F 16/32/64GB RAM RTX 5060 Ti 8GB GAMER PC termékbeszámítással
- ÁRGARANCIA!Épített KomPhone i7 14700KF 32/64GB RAM RX 9070 16GB GAMER PC termékbeszámítással
- BESZÁMÍTÁS! Acer Predator Helios Neo 16 PHN16 notebook-i9 13900HX 16GB DDR5 1TB SSD RTX 4060 8GB W11
- ÁRGARANCIA!Épített KomPhone i9 14900KF 64GB RAM RTX 5080 16GB GAMER PC termékbeszámítással
Állásajánlatok
Cég: Laptopszaki Kft.
Város: Budapest
Cég: PCMENTOR SZERVIZ KFT.
Város: Budapest